Understand Check if Grid can be Cut into Sections Problem

Problem Name: Check if Grid can be Cut into Sections
Problem Description:

Check if Grid can be Cut into Sections

Problem Description

You are given an integer n representing the dimensions of an n x n grid, with the origin at the bottom-left corner of the grid. You are also given a 2D array of coordinates rectangles, where rectangles[i] = [startx, starty, endx, endy] represents a rectangle on the grid. Each rectangle is defined as follows:

  • (startx, starty): The bottom-left corner of the rectangle.
  • (endx, endy): The top-right corner of the rectangle.

Conditions to Satisfy:

Your task is to determine if it is possible to make either two horizontal or two vertical cuts on the grid such that:

  1. Each of the three resulting sections formed by the cuts contains at least one rectangle.
  2. Every rectangle belongs to exactly one section (i.e., no rectangle spans across a cut).

Return:

  • true if such cuts can be made.
  • false otherwise.

Examples & Explanation

Example 1

Input:

n = 5
rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]

Grid Representation:

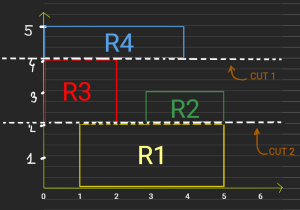
FDSSD

Explanation:

We can make horizontal cuts at y = 2 and y = 4, forming three sections:

  • Section 1: Below y = 2 (contains R1)
  • Section 2: Between y = 2 and y = 4 (contains R2 and R3)
  • Section 3: Above y = 4 (contains R4)

Since all conditions are satisfied, output is true.

Constraints

3≤n≤1093 \leq n \leq 10^9 3≤rectangles.length≤1053 \leq \text{rectangles.length} \leq 10^5 0≤rectangles[i][0]<rectangles[i][2]≤n0 \leq \text{rectangles}[i][0] < \text{rectangles}[i][2] \leq n 0≤rectangles[i][1]<rectangles[i][3]≤n0 \leq \text{rectangles}[i][1] < \text{rectangles}[i][3] \leq n

Rectangles do not overlap.

Category:
  • Arrays
  • Sorting
Programming Language:
  • Java
Reference Link:

https://leetcode.com/problems/check-if-grid-can-be-cut-into-sections/description/

Online IDE

Scroll down for output
Java
Output:
Loading component...
Loading component...
Tracking code (View only. In case you want to track the code, click this button):
Main Function:
INPUT: n = 5;  rectangles = {{1,0,5,2},{0,2,2,4},{3,2,5,3},{0,4,4,5}};
OUTPUT: True
    public static void main(String[] args) {
 int n = 5;
 int[][] rectangles = {{1,0,5,2},{0,2,2,4},{3,2,5,3},{0,4,4,5}};
boolean checkValidCuts = checkValidCuts(n, rectangles);
if (checkValidCuts) {
 System.out.println("cuts can be made");
}//If End
else{
System.out.println("cuts cannot be made");
}//Else End
}//Function End
Helper Function:
public static boolean checkValidCuts(int n, int[][] rectangles) {
 int[][] xIntervals = new int[rectangles.length][2];
int[][] yIntervals = new int[rectangles.length][2];
for (int i = 0; i < rectangles.length; i++) {
xIntervals[i][0] = rectangles[i][0];
  xIntervals[i][1] = rectangles[i][2];
 yIntervals[i][0] = rectangles[i][1];
 yIntervals[i][1] = rectangles[i][3];
}//Loop End
boolean f1 = check(xIntervals);
boolean f2 = check(yIntervals);
return f1 || f2 ;
}//Function End
Utility Functions and Global variables:
private static boolean check(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
int sections = 0;
        int maxEnd = intervals[0][1];
 for (int[] interval : intervals) {
if (maxEnd <= interval[0]) {
sections++;
}//If End
 maxEnd = Math.max(maxEnd, interval[1]);
}//Loop End
return sections >= 2;
}//Function End
Privacy Policy | About