Understand Recover From Preorder Traversal Problem

Problem Name: Recover From Preorder Traversal
Problem Description:

Recover From Preorder Traversal

Problem Statement

You are given a string representing the preorder depth-first search (DFS) traversal of a binary tree. In this traversal, each node is output as a series of dashes followed by its integer value. The number of dashes indicates the node's depth in the tree:

  • The root node (depth 0) is printed without any dashes.
  • For any node at depth D, its children are printed with D+1 leading dashes.
  • Note: If a node has only one child, it is guaranteed to be the left child.

Your task is to reconstruct the original binary tree from this traversal string and return the tree's root.

Task

Implement a function that, given the preorder traversal string, recovers the binary tree and returns its root.

Test Cases

Example 1

Input:
traversal = "10-20--30--40-50--60--70" graph Output:
[10, 20, 50, 30, 40, 60, 70]

Explanation:

  • The root is 10.
  • 20 is the left child of 10.
  • 30 and 40 are the left and right children of 20, respectively.
  • 50 is the right child of 10.
  • 60 and 70 are the left and right children of 50, respectively.

Example 2

Input:
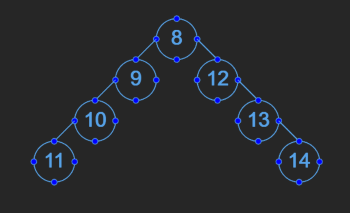
traversal = "8-9--10---11-12--13---14" [8, 9, 12, 10, null, 13, null, 11, null, 14] graph Explanation:

  • The root is 8.
  • 9 is the left child of 8.
  • 10 is the left child of 9.
  • 11 is the left child of 10.
  • 12 is the right child of 8.
  • 13 is the left child of 12.
  • 14 is the left child of 13.

Example 3

Input:
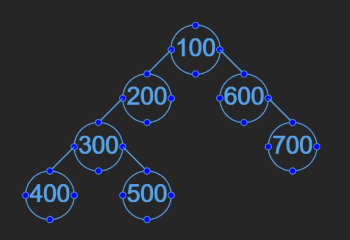
traversal = "100-200--300---400---500-600--700" graph Output: [100, 200, 600, 300, null, 700, null, 400, 500]

Explanation:

  • The root is 100.
  • 200 is the left child of 100.
  • 300 is the left child of 200.
  • 400 and 500 are the left and right children of 300, respectively.
  • 600 is the right child of 100.
  • 700 is the left child of 600.

Constraints

  • The number of nodes in the original tree is in the range [1, 1000].
  • 1 <= Node.val <= 10⁹

Approach

  1. Parse the Traversal String:
    • Read the string sequentially.
    • Count the number of consecutive dashes to determine the depth of the current node.
    • Parse the following digits to form the node's value.
  2. Construct the Tree:
    • Use a stack to maintain nodes along the current path.
    • For each node encountered, compare its depth with the depth of the node on the top of the stack.
    • If the current node’s depth is greater, it is the left child of the previous node; otherwise, backtrack in the stack to find the correct parent and attach it as a right child.
  3. Return the Root:
    • After processing the entire string, the first element in the stack (or stored separately) will be the root of the reconstructed binary tree.
Category:
  • Leetcode Problem of the Day
  • Binary Trees
Programming Language:
  • Java
Reference Link:

https://leetcode.com/problems/recover-a-tree-from-preorder-traversal/description

Online IDE

Scroll down for output
Java
Output:
Loading component...
Loading component...
Tracking code (View only. In case you want to track the code, click this button):
Main Function:
Main Function is not defined.
Helper Function:
INPUT: 10-20--30--40-50--60--70
OUTPUT: [10, 20, 50, 30, 40, 60, 70]
public TreeNode recoverFromPreorder(String traversal) {
Stack<TreeNode> stack = new Stack<>();
int i = 0;
int n = traversal.length();
while (i < n) {
int depth = 0;
while (i < n && traversal.charAt(i) == '-') {
depth++;
i++;
}//Loop End
int value = 0;
while (i < n && Character.isDigit(traversal.charAt(i))) {
value = value * 10 + (traversal.charAt(i) - '0');
i++;
}//Loop End
TreeNode node = new TreeNode(value);
 while (stack.size() > depth) {
 stack.pop();
}//Loop End
if (!stack.isEmpty()) {
 TreeNode parent = stack.peek();
if (parent.left == null) {
parent.left = node; 
}//If End
else {
 parent.right = node;
}//Else End
}//If End
 stack.push(node);
}//Loop End
 while (stack.size() > 1) {
stack.pop();
}//Loop End
 return stack.peek();
}//function end
Utility Functions and Global variables:
Utility Function is not required.
Privacy Policy | About