Problem Name: Bellman-Ford Algorithm
Problem Description:
Bellman-Ford Algorithm
The Bellman-Ford Algorithm is a graph algorithm used to find the shortest path from a single source vertex to all other vertices in a weighted graph. It is particularly useful when the graph contains negative weight edges.
Algorithm Steps
- Initialize distances:
- Set the distance to the source vertex as
0and all other vertices as∞(infinity).
- Set the distance to the source vertex as
- Relax edges (V - 1) times:
- Iterate over all edges and update the distance to each vertex if a shorter path is found.
- Check for negative-weight cycles:
- Run one more iteration over all edges.
- If any distance can still be reduced, the graph contains a negative-weight cycle.
Complexity Analysis
Time Complexity:
- The algorithm runs (V - 1) iterations, where each iteration processes E edges.
- This results in a time complexity of O(VE), making it slower than Dijkstra's algorithm for dense graphs.
Space Complexity:
- The algorithm requires an array to store distances, leading to a space complexity of O(V).
Applications
Detecting Negative-Weight Cycles
The Bellman-Ford algorithm can detect negative-weight cycles, which are cycles in a graph where the sum of edge weights is negative. If such a cycle exists, the algorithm reports it, preventing incorrect shortest path calculations.
Shortest Path Calculation
Bellman-Ford is useful for finding the shortest path in graphs that contain negative-weight edges, unlike Dijkstra’s algorithm, which fails with negative weights.
Routing Protocols
The algorithm is used in network routing protocols such as RIP (Routing Information Protocol) to find the shortest paths in a network.
Example Graph
Consider the following weighted directed graph:
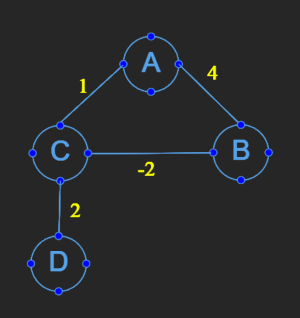
A --(4)--> B
A --(1)--> C
B --(-2)--> C
C --(2)--> D
If A is the source vertex, the Bellman-Ford algorithm computes the shortest paths from A to all other vertices, considering both positive and negative edge weights.
OUTPUT: Shortest distances from source 0: To vertex 0 is 0 To vertex 1 is 6 To vertex 2 is 7 To vertex 3 is 2 To vertex 4 is 4
Category:- Graphs
- Searching
Programming Language: - Java
Reference Link:
https://drawtocode.vercel.app/problems/bellman-ford-algorithm
Online IDE
Scroll down for outputLoading component...
Loading component...
Tracking code (View only. In case you want to track the code, click this button):
Main Function:
INPUT: A --(4)--> B ,A --(1)--> C , B --(-2)--> C , C --(2)--> D
OUTPUT: {0: 0, 1: 4, 2: 1, 3: 3}
public static void main(String[] args) {
int vertices = 5;
List<Edge> edges = new ArrayList<>();
edges.add(new Edge(0, 1, 6));
edges.add(new Edge(0, 2, 7));
edges.add(new Edge(1, 2, 8));
edges.add(new Edge(1, 3, -4));
edges.add(new Edge(1, 4, 5));
edges.add(new Edge(2, 3, 9));
edges.add(new Edge(2, 4, -3));
edges.add(new Edge(3, 1, 7));
edges.add(new Edge(4, 0, 2));
edges.add(new Edge(4, 3, 7));
int source = 0;
int[] distances = bellmanFord(vertices, edges, source);
if (distances != null) {
System.out.println("Shortest distances from source " + source + ":");
for (int i = 0; i < vertices; i++) {
System.out.println("To vertex " + i + " is " + distances[i]);
}//Loop End
}//If End
} //Function End
Helper Function:
public static int[] bellmanFord(int vertices, List<Edge> edges, int source) {
int[] dist = new int[vertices];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[source] = 0;
for (int i = 0; i < vertices - 1; i++) {
for (Edge edge : edges) {
if (dist[edge.from] != Integer.MAX_VALUE && dist[edge.from] + edge.weight < dist[edge.to]) {
dist[edge.to] = dist[edge.from] + edge.weight;
}
} // Loop end
} //Loop end
for (Edge edge : edges) {
if (dist[edge.from] != Integer.MAX_VALUE && dist[edge.from] + edge.weight < dist[edge.to]) {
System.out.println("Graph contains a negative weight cycle");
return null;
}
} //Loop end
return dist;
} //function end
Utility Functions and Global variables:
public static class Edge {
int from, to, weight;
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
} }