Understand Dijkstras Algorithm Problem

Problem Name: Dijkstras Algorithm
Problem Description:

Dijkstra’s Algorithm (Shortest Path)

Dijkstra’s algorithm is a classic method for finding the shortest path from a starting node to every other node in a weighted graph (with non-negative edge weights).

How It Works

  1. Initialization
    • Distance Map: Create an object dist where every node’s distance is set to infinity (∞), except the start node which is set to 0.
    • Priority Queue: Use a priority queue (or min-heap) to store nodes ordered by their current shortest distance.
    • Previous Map: Optionally, maintain a previous map to keep track of the best preceding node for each node (useful for reconstructing the shortest path).
  2. Main Loop
    While the priority queue is not empty:
    • Extract Minimum: Remove the node u with the smallest distance from the queue.
    • Relaxation: For each neighbour v of u:
      • Compute an alternative distance:
        alt = dist[u] + weight(u, v)
      • If alt is less than dist[v]:
        • Update dist[v] to alt.
        • Set previous[v] to u.
        • Add or update v in the priority queue with the new distance.
  3. Result Extraction
    • After processing, the dist object contains the shortest distances from the start node to every other node.
    • To reconstruct the shortest path from the start node to a target node, backtrack using the previous map.

Example Graph

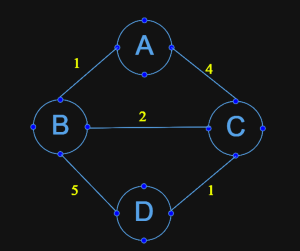
Consider the following graph: dijkstra

  • Edges:
    • A → B (weight = 1)
    • A → C (weight = 4)
    • B → C (weight = 2)
    • B → D (weight = 5)
    • C → D (weight = 1)

Goal: Find the shortest path from node A to node D.

Step-by-Step Execution

  1. Initialization:
    • dist = { A: 0, B: ∞, C: ∞, D: ∞ }
    • previous = {}
    • Priority Queue: [(A, 0)]
  2. Processing Node A:
    • Dequeue A (distance = 0).
    • For neighbour B:
      • alt = 0 + 1 = 1 → Update dist[B] = 1, previous[B] = A.
    • For neighbour C:
      • alt = 0 + 4 = 4 → Update dist[C] = 4, previous[C] = A.
    • Queue becomes: [(B, 1), (C, 4)].
  3. Processing Node B:
    • Dequeue B (distance = 1).
    • For neighbour C:
      • alt = 1 + 2 = 3 → Update dist[C] = 3, previous[C] = B.
    • For neighbour D:
      • alt = 1 + 5 = 6 → Update dist[D] = 6, previous[D] = B.
    • Queue becomes: [(C, 3), (C, 4), (D, 6)]
      (Duplicates in the queue are handled appropriately in a proper priority queue implementation.)
  4. Processing Node C:
    • Dequeue C (distance = 3).
    • For neighbour D:
      • alt = 3 + 1 = 4 → Update dist[D] = 4, previous[D] = C.
    • Queue becomes: [(D, 4), (D, 6)].
  5. Processing Node D:
    • Dequeue D (distance = 4).
    • D has no neighbours needing updates.
    • The queue is now empty.
  6. Reconstructing the Shortest Path from A to D:
    • Start at D: previous[D] = C
    • Then C: previous[C] = B
    • Then B: previous[B] = A
    • Path: A → B → C → D with a total distance of 4.
Category:No additional categories provided
Programming Language:
  • Java
Reference Link:

https://drawtocode.vercel.app/problems/dijkstras-algorithm

Online IDE

Scroll down for output
Java
Output:
Loading component...
Loading component...
Tracking code (View only. In case you want to track the code, click this button):
Main Function:
INPUT : graph = {     'A': [('B', 1), ('C', 4)],     'B': [('A', 1), ('C', 2), ('D', 5)],     'C': [('A', 4), ('B', 2), ('D', 1)],     'D': [('B', 5), ('C', 1)] }
OUTPUT: Shortest paths from A:      A : 0 B : 1 C : 3 D : 4
public static void main(String[] args) {
 Map<String, List<Node>> graph = new HashMap<>();
graph.put("A", Arrays.asList(new Node("B", 1), new Node("C", 4)));
graph.put("B", Arrays.asList(new Node("A", 1), new Node("C", 2), new Node("D", 5)));
graph.put("C", Arrays.asList(new Node("A", 4), new Node("B", 2), new Node("D", 1)));
graph.put("D", Arrays.asList(new Node("B", 5), new Node("C", 1)));
String start = "A";
Map<String, Integer> shortestPaths = dijkstra(graph, start);
 System.out.println("Shortest paths from " + start + ":");
for (Map.Entry<String, Integer> entry : shortestPaths.entrySet()) {
System.out.println(entry.getKey() + " : " + entry.getValue());
}//Loop End
}//function end
Helper Function:
public static Map<String, Integer> dijkstra(Map<String, List<Node>> graph, String start) {
 Map<String, Integer> distances = new HashMap<>();
 for (String vertex : graph.keySet()) {
distances.put(vertex, Integer.MAX_VALUE);
} //Loop End 
 distances.put(start, 0);
PriorityQueue<Node> queue = new PriorityQueue<>();
 queue.add(new Node(start, 0));
while (!queue.isEmpty()) {
Node current = queue.poll();
String currentVertex = current.vertex;
int currentDistance = current.distance;
 if (currentDistance > distances.get(currentVertex)) {
continue;
}
for (Node neighbor : graph.get(currentVertex)) {
int distanceThroughCurrent = currentDistance + neighbor.distance;
 if (distanceThroughCurrent < distances.get(neighbor.vertex)) {
distances.put(neighbor.vertex, distanceThroughCurrent);
  queue.add(new Node(neighbor.vertex, distanceThroughCurrent));
}
 }//Loop end
 }//Loop end
return distances;
}//function end
Utility Functions and Global variables:
static class Node implements Comparable<Node> {
public String vertex;
public int distance;
public Node(String vertex , int distance) {
this.vertex = vertex;
this.distance = distance;
}
@Override
public int compareTo(Node other) {
return this.distance - other.distance;
}
} // Class End
Privacy Policy | About