Find the Minimum Area to Cover All Ones II

Difficulty: Hard

You are given a 2D binary array grid. You need to find three non-overlapping rectangles (axis-aligned, non-zero area) such that all the 1s in grid lie inside these rectangles.

Return the minimum possible sum of the areas of these rectangles.

Note: Rectangles are allowed to touch (share borders or corners), but they must not overlap in area.

---

Examples

Example 1

Input:

grid = [[1,0,1],
        [1,1,1]]

Output:

5

Explanation:

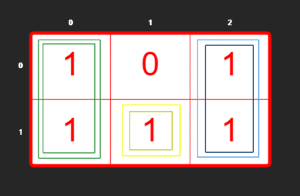
• The 1s at (0,0) and (1,0) are covered by a rectangle of area 2.
• The 1s at (0,2) and (1,2) are covered by a rectangle of area 2.
• The 1 at (1,1) is covered by a rectangle of area 1.
• Total area = 2 + 2 + 1 = 5.

---

Example 2

Input:

grid = [[1,0,1,0],
        [0,1,0,1]]

Output:

5

Explanation:

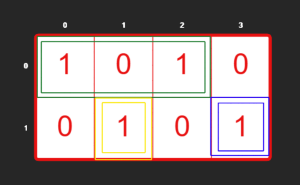
• The 1s at (0,0) and (0,2) are covered by a rectangle of area 3.
• The 1 at (1,1) is covered by a rectangle of area 1.
• The 1 at (1,3) is covered by a rectangle of area 1.
• Total area = 3 + 1 + 1 = 5.

---

Constraints

• 1 <= grid.length, grid[i].length <= 30
• grid[i][j] is either 0 or 1.
• The input is generated such that there are at least three 1s in grid.