Kruskal’s Algorithm (Minimum Spanning Tree)

Kruskal’s Algorithm is a greedy algorithm used to construct a Minimum Spanning Tree (MST) from a weighted, undirected graph. The goal of the MST is to connect all vertices with the minimum total edge weight, without forming any cycles.

---

How It Works

1. Sort All Edges:
   Begin by sorting all the edges in the graph in non-decreasing order by their weights.
2. Initialize MST:
   Start with an empty set that will eventually become your MST. Each vertex is initially in its own separate tree.
3. Edge Selection:
   Iterate over the sorted edges and, for each edge, check if including it in the MST would create a cycle.
   • Cycle Detection:
     This is typically done using a Union-Find (Disjoint Set Union) data structure.
     • If the two endpoints of the edge belong to different sets, the edge can be safely added to the MST, and the sets are merged.
     • If the endpoints are in the same set, adding the edge would form a cycle, so it is skipped.
4. Repeat Until Completion:
   Continue adding edges until the MST contains exactly (V - 1) edges, where (V) is the number of vertices in the graph.

---

Example

Consider a graph with 5 vertices labeled A, B, C, D, and E and the following weighted edges:

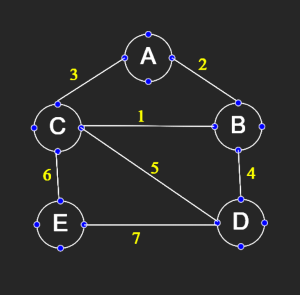
• Edge (A, B) with weight 2
• Edge (A, C) with weight 3
• Edge (B, C) with weight 1
• Edge (B, D) with weight 4
• Edge (C, D) with weight 5
• Edge (C, E) with weight 6
• Edge (D, E) with weight 7

Step-by-Step Process:

1. Sort the Edges:
   Sorted by weight (lowest to highest):
   [ {   (B, C): 1,   (A, B): 2,   (A, C): 3,   (B, D): 4,   (C, D): 5,   (C, E): 6,   (D, E): 7 } ]
2. Initialize MST:
   Start with an empty MST. Each vertex (A, B, C, D, E) is in its own component.
3. Process Each Edge:
   • Edge (B, C) (weight 1):
     Vertices B and C are in different components. Include this edge.
   • Edge (A, B) (weight 2):
     Vertices A and B are in different components. Include this edge.
   • Edge (A, C) (weight 3):
     Now A, B, and C are already connected. Including (A, C) would form a cycle, so skip it.
   • Edge (B, D) (weight 4):
     Vertex D is not yet connected to the MST containing A, B, C. Include this edge.
   • Edge (C, D) (weight 5):
     Both C and D are already connected. Skip to avoid cycle.
   • Edge (C, E) (weight 6):
     Vertex E is not connected. Include this edge.
   • Edge (D, E) (weight 7):
     Both D and E are now connected in the MST; skip it.
4. MST Formed:
   The MST consists of the edges:
   • (B, C): 1
   • (A, B): 2
   • (B, D): 4
   • (C, E): 6
     Total Weight: (1 + 2 + 4 + 6 = 13)

---

Summary

Kruskal’s Algorithm constructs the Minimum Spanning Tree by:

• Sorting all edges by weight.
• Iteratively adding the smallest edge that does not form a cycle.
• Using a Union-Find structure to efficiently check for cycles.

This greedy approach guarantees that the final tree spans all vertices with the minimum possible total weight.

Complexity

• Time Complexity:

$$O(E \log E) \quad (\text{approximately } O(E \log V))$$

(Sorting the edges dominates; union-find operations are nearly constant time.)

• Space Complexity:

$$O(V + E)$$

(Space is used to store the edge list and the union-find structure.)