Kruskal’s Algorithm (Minimum Spanning Tree)
Kruskal’s Algorithm is a greedy algorithm used to construct a Minimum Spanning Tree (MST) from a weighted, undirected graph. The goal of the MST is to connect all vertices with the minimum total edge weight, without forming any cycles.
How It Works
- Sort All Edges:
Begin by sorting all the edges in the graph in non-decreasing order by their weights. - Initialize MST:
Start with an empty set that will eventually become your MST. Each vertex is initially in its own separate tree. - Edge Selection:
Iterate over the sorted edges and, for each edge, check if including it in the MST would create a cycle.- Cycle Detection:
This is typically done using aUnion-Find(Disjoint Set Union) data structure.- If the two endpoints of the edge belong to different sets, the edge can be safely added to the MST, and the sets are merged.
- If the endpoints are in the same set, adding the edge would form a cycle, so it is skipped.
- Cycle Detection:
- Repeat Until Completion:
Continue adding edges until the MST contains exactly (V - 1) edges, where (V) is the number of vertices in the graph.
Example
Consider a graph with 5 vertices labeled A, B, C, D, and E and the following weighted edges:
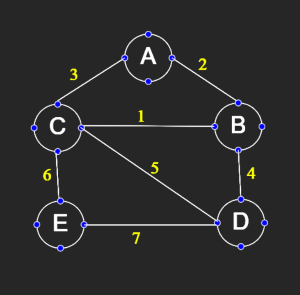
- Edge
(A, B)with weight 2 - Edge
(A, C)with weight 3 - Edge
(B, C)with weight 1 - Edge
(B, D)with weight 4 - Edge
(C, D)with weight 5 - Edge
(C, E)with weight 6 - Edge
(D, E)with weight 7
Step-by-Step Process:
- Sort the Edges:
Sorted by weight (lowest to highest):
[ {(B, C): 1,(A, B): 2,(A, C): 3,(B, D): 4,(C, D): 5,(C, E): 6,(D, E): 7 } ] - Initialize MST:
Start with an empty MST. Each vertex (A, B, C, D, E) is in its own component. - Process Each Edge:
- Edge
(B, C)(weight 1):
Vertices B and C are in different components. Include this edge. - Edge
(A, B)(weight 2):
Vertices A and B are in different components. Include this edge. - Edge
(A, C)(weight 3):
Now A, B, and C are already connected. Including (A, C) would form a cycle, so skip it. - Edge
(B, D)(weight 4):
Vertex D is not yet connected to the MST containing A, B, C. Include this edge. - Edge
(C, D)(weight 5):
Both C and D are already connected. Skip to avoid cycle. - Edge
(C, E)(weight 6):
Vertex E is not connected. Include this edge. - Edge
(D, E)(weight 7):
Both D and E are now connected in the MST; skip it.
- Edge
- MST Formed:
The MST consists of the edges:(B, C): 1(A, B): 2(B, D): 4(C, E): 6
Total Weight: (1 + 2 + 4 + 6 = 13)
Summary
Kruskal’s Algorithm constructs the Minimum Spanning Tree by:
- Sorting all edges by weight.
- Iteratively adding the smallest edge that does not form a cycle.
- Using a Union-Find structure to efficiently check for cycles.
This greedy approach guarantees that the final tree spans all vertices with the minimum possible total weight.
Complexity
- Time Complexity:
(Sorting the edges dominates; union-find operations are nearly constant time.)
- Space Complexity:
(Space is used to store the edge list and the union-find structure.)
Category:- Graphs
Programming Language: - Java
Reference Link:
https://drawtocode.vercel.app/problems/kruskal’s-algorithm
Loading component...
Loading component...