Understand Prims Algorithm Problem

Problem Name: Prims Algorithm
Problem Description:

Prim’s Algorithm (Minimum Spanning Tree)

Prim’s algorithm is a greedy method for finding a Minimum Spanning Tree (MST) in a weighted, undirected graph. An MST is a subset of the graph’s edges that connects all vertices together without any cycles and with the minimum possible total edge weight.

How It Works

  1. Initialization:
    • Start from an arbitrary vertex and mark it as part of the MST.
    • Maintain two sets of vertices: one included in the MST and the other not yet included.
  2. Selection of Edge:
    • At each step, look for the smallest weighted edge that connects a vertex in the MST to a vertex outside the MST.
    • Add both the edge and the connected vertex to the MST.
  3. Repeat:
    • Continue this process until all vertices are included in the MST.

The algorithm always picks the next minimum edge that expands the growing tree, ensuring that the total weight remains as low as possible.

Example

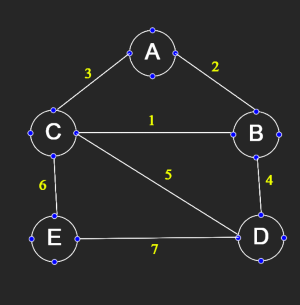prims graph Consider a graph with 5 vertices labeled A, B, C, D, and E with the following weighted edges:

  • Edge (A, B) with weight 2
  • Edge (A, C) with weight 3
  • Edge (B, C) with weight 1
  • Edge (B, D) with weight 4
  • Edge (C, D) with weight 5
  • Edge (C, E) with weight 6
  • Edge (D, E) with weight 7

Step-by-Step Process:

  1. Start at Vertex A:
    • MST Set: {A}
    • Outgoing edges from A:
      • (A, B): weight 2
      • (A, C): weight 3
    • Choose: (A, B) because 2 is the minimum.
    • MST now contains: A, B and edge (A, B).
  2. Expand the MST (Now contains A, B):
    • Look at edges from A and B to vertices not yet in the MST:
      • From A: (A, C) with weight 3
      • From B: (B, C) with weight 1 and (B, D) with weight 4
    • Choose: (B, C) with weight 1.
    • MST now contains: A, B, C and edges (A, B), (B, C).
  3. Continue Expanding (MST now: A, B, C):
    • Consider edges from the current MST to outside vertices:
      • From B: (B, D) with weight 4
      • From C: (C, D) with weight 5 and (C, E) with weight 6
    • Choose: (B, D) with weight 4.
    • MST now contains: A, B, C, D and edges (A, B), (B, C), (B, D).
  4. Final Expansion (MST now: A, B, C, D):
    • The only vertex left is E.
    • Consider edges connecting to E:
      • From C: (C, E) with weight 6
      • From D: (D, E) with weight 7
    • Choose: (C, E) with weight 6.
    • MST now contains: A, B, C, D, E and edges (A, B), (B, C), (B, D), (C, E).

Final MST:

  • Edges: (A, B): 2, (B, C): 1, (B, D): 4, (C, E): 6
  • Total Weight: (2 + 1 + 4 + 6 = 13)

Summary

Prim’s Algorithm builds a minimum spanning tree by starting from an arbitrary vertex and, at each step, adding the least expensive edge that connects a vertex in the tree to a vertex outside it. This process continues until all vertices are included in the tree, ensuring the total edge weight is minimized.

Category:
  • Graphs
Programming Language:
  • Java
Reference Link:

https://drawtocode.vercel.app/problems/prims-algorithm

Online IDE

Scroll down for output
Java
Output:
Loading component...
Loading component...
Tracking code (View only. In case you want to track the code, click this button):
Main Function:
INPUT graph = INPUT: graph = {{  0,  2,  3,  0,  0},  {  2,  0,  1,  4,  0}, {  3,  1,  0,  5,  6},{  0,  4,  5,  0,  7},  {  0,  0,  6,  7,  0} };
OUTPUT:  A - B   ( 2 )   B - C  ( 1)   B - D ( 4)   C - E  ( 6 )
    public static void main (String[] args) {
V = 3;
 graph = new int[][] {{0,1,5},{1,2,3},  {0,2,1}};
primMST();
}//Function End
Helper Function:
public static void primMST() {
int[] parent = new int[V];
int[] key = new int[V];
boolean[] mstSet = new boolean[V];
Arrays.fill(key, INF);
 key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}//If End
}//Loop End
}//Loop End
printMST(parent);
}//function end
Utility Functions and Global variables:
static final int INF = 99999;
static int V; // Number of vertices
static int[][] graph; // Adjacency matrix
 private static int minKey(int[] key, boolean[] mstSet) {
 int min = INF, minIndex = -1;
 for (int v = 0; v < V; v++) {
if (!mstSet[v] && key[v] < min) {
   min = key[v];
minIndex = v;
}//If End
}//Loop End
 return minIndex;
}//function end
    static void printMST(int[] parent){
System.out.println("Edge 	Weight");
 for (int i = 1; i < V; i++) {
 System.out.println(parent[i] + " - " + i + "	" + graph[i][parent[i]]);
}//Loop End
System.out.println();
} // Function End
Privacy Policy | About